Algorithms

Algorithms

Radix Sort

Radix sort is based on the idea that the sorting of the input data is done digit by digit from least significant digit to most significant digit and it uses counting sort as a subroutine to perform sorting. Counting sort is a linear sorting algorithm with overall time complexity Θ(N+K) in all cases, where N is the number of elements in the unsorted array and K is the range of input data. The idea of radix sort is to extend the counting sort algorithm to get a better time complexity when K goes up.

Example:

To understand the radix sort, lets consider an unsorted array A = [101, 1, 20, 50, 9, 98, 27, 153, 35, 899] and discuss each step taken to sort the array in ascending order.

Step 1: According to the algorithms, the input data is first sorted based on least significant digit. Therefore, array A[ ] is sorted based on one's digit. After sorting it on one's digit it will become [20, 50, 101, 1, 153, 35, 27, 98, 9, 899].

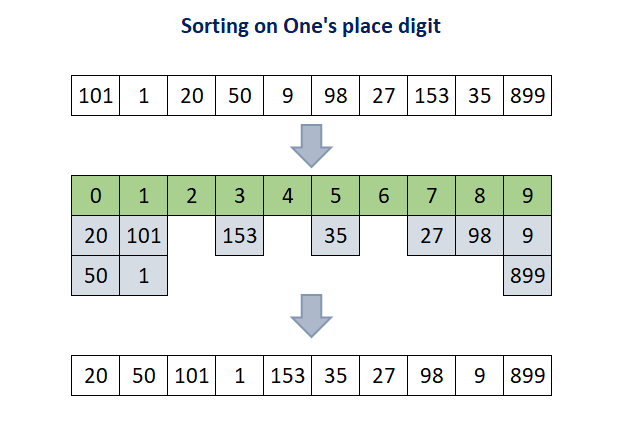
Radix Sort

Step 2: In this step, the array A[ ] array is sorted based on ten's digit and after this step it will become [101, 1, 9, 20, 27, 35, 50, 153, 98, 899].

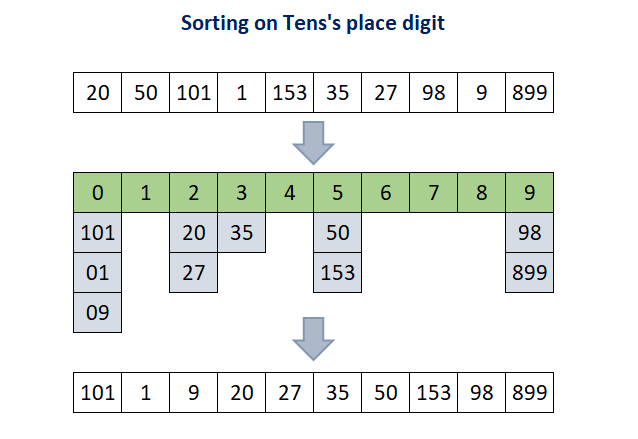
Radix Sort

Step 3: Finally, the array A[ ] is sorted based on hundred's digit (most significant digit) and the array will be sorted after this step and the final array will be [1, 9, 20, 27, 35, 50, 98, 101, 153, 899].

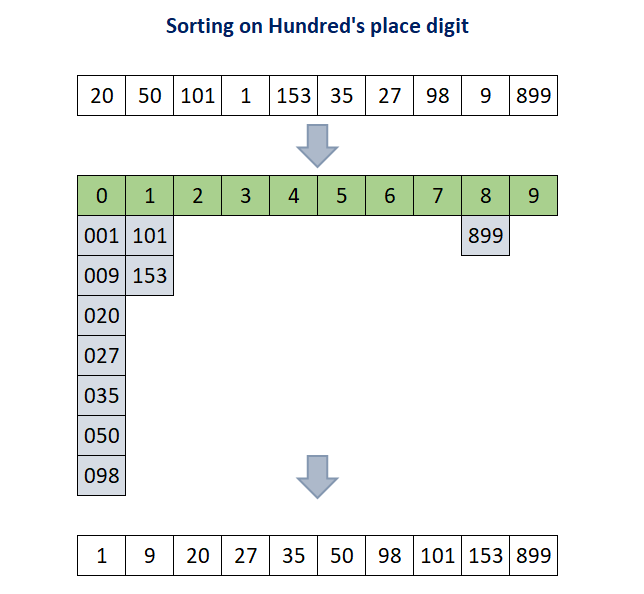
Radix Sort

Implementation of Radix Sort

# function for radix sort
def radixsort(MyList):
  n = len(MyList)
  max = MyList[0]
  
  #find largest element in the Array
  for i in MyList:
    if max < i:
      max = i
  
  #Counting sort is performed based on place. 
  #like ones place, tens place and so on.
  place = 1
  while max/place > 0:
    countingsort(MyList, place)
    place *= 10  

def countingsort(MyList, place):
  n = len(MyList)
  output = [0 for i in range(0,n)]
  
  #range of the number is 0-9 for each place considered.
  freq = [0 for i in range(0,10)]
  
  #count number of occurrences in freq array
  for i in range(0,n):
    freq[(MyList[i]//place)%10] += 1
  
  #Change count[i] so that count[i] now contains actual 
  #position of this digit in output[] 
  for i in range(1,10):
    freq[i] += freq[i - 1]      
  
  #Build the output array 
  for i in range(n-1,-1,-1):
    output[freq[(MyList[i]//place)%10] - 1] = MyList[i] 
    freq[(MyList[i]//place)%10] -= 1
  
  #Copy the output array to the input Array, Now the Array will 
  #contain sorted array based on digit at specified place
  for i in range(0,n): 
    MyList[i] = output[i]   

#print a list
def PrintList(MyList):
  for i in MyList:
    print(i, end=" ")
  print("\n") 
  
# test the code                 
MyList = [101, 1, 20, 50, 9, 98, 27, 153, 35, 899]
print("Original List")
PrintList(MyList)

radixsort(MyList)
print("Sorted List")
PrintList(MyList)

The above code will give the following output:

Original List
101 1 20 50 9 98 27 153 35 899 

Sorted List
1 9 20 27 35 50 98 101 153 899

public class MyClass {
  // function for radix sort
  static void radixsort(int Array[]) {
    int n = Array.length;
    int max = Array[0];

    //find largest element in the Array
    for (int i=1; i<n; i++) {  
      if(max < Array[i])
        max = Array[i];
    }

    //Counting sort is performed based on place. 
    //like ones place, tens place and so on.
    for (int place = 1; max/place > 0; place *= 10) 
      countingsort(Array, place); 
  }

  static void countingsort(int Array[], int place) {   
    int n = Array.length;    
    int[] output = new int[n];

    //range of the number is 0-9 for each place considered.
    int[] freq = {0, 0, 0, 0, 0, 0, 0, 0, 0, 0};

    //count number of occurrences in freq array
    for(int i = 0; i < n; i++)
      freq[(Array[i]/place)%10]++;

    //Change count[i] so that count[i] now contains actual 
    //position of this digit in output[] 
    for (int i = 1; i < 10; i++) 
      freq[i] += freq[i - 1];    

    //Build the output array 
    for (int i = n - 1; i >= 0; i--) { 
      output[freq[(Array[i]/place)%10] - 1] = Array[i]; 
      freq[(Array[i]/place)%10]--; 
    } 
  
    //Copy the output array to the input Array, Now the Array will 
    //contain sorted array based on digit at specified place
    for (int i = 0; i < n; i++) 
      Array[i] = output[i]; 
  }

  // function to print array
  static void PrintArray(int Array[]) { 
    int n = Array.length; 
    for (int i=0; i<n; i++)  
      System.out.print(Array[i] + " "); 
    System.out.println(); 
  } 

  // test the code
  public static void main(String[] args) {
    int[] MyArray =  {101, 1, 20, 50, 9, 98, 27, 153, 35, 899};
    System.out.println("Original Array");
    PrintArray(MyArray);

    radixsort(MyArray);
    System.out.println("\nSorted Array");
    PrintArray(MyArray);  
  }
}

The above code will give the following output:

Original Array
101 1 20 50 9 98 27 153 35 899 

Sorted Array
1 9 20 27 35 50 98 101 153 899

#include <iostream>
using namespace std;

static void radixsort(int Array[], int n);
static void countingsort(int Array[], int n, int place);
static void PrintArray(int Array[], int n); 

// function for radix sort
void radixsort(int Array[], int n) {
  int max = Array[0];

  //find largest element in the Array
  for (int i=1; i<n; i++) {  
    if(max < Array[i])
      max = Array[i];
  }

  //Counting sort is performed based on place. 
  //like ones place, tens place and so on.
  for (int place = 1; max/place > 0; place *= 10) 
    countingsort(Array, n, place); 
}

static void countingsort(int Array[], int n, int place) {   
  int output[n];
  //range of the number is 0-9 for each place considered.
  int freq[10] = {0};

  //count number of occurrences in freq array
  for(int i = 0; i < n; i++)
    freq[(Array[i]/place)%10]++;

  //Change count[i] so that count[i] now contains actual 
  //position of this digit in output[] 
  for (int i = 1; i < 10; i++) 
    freq[i] += freq[i - 1];    

  //Build the output array 
  for (int i = n - 1; i >= 0; i--) { 
    output[freq[(Array[i]/place)%10] - 1] = Array[i]; 
    freq[(Array[i]/place)%10]--; 
  }   

  //Copy the output array to the input Array, Now the Array will 
  //contain sorted array based on digit at specified place
  for (int i = 0; i < n; i++) 
    Array[i] = output[i]; 
}

// function to print array
static void PrintArray(int Array[], int n) { 
  for (int i=0; i<n; i++) 
    cout<<Array[i]<<" "; 
  cout<<"\n"; 
} 

// test the code
int main () {
  int MyArray[] = {101, 1, 20, 50, 9, 98, 27, 153, 35, 899};
  int n = sizeof(MyArray) / sizeof(MyArray[0]); 
  cout<<"Original Array\n";
  PrintArray(MyArray, n);


  radixsort(MyArray, n);
  cout<<"\nSorted Array\n";
  PrintArray(MyArray, n);
  return 0;
}

The above code will give the following output:

Original Array
101 1 20 50 9 98 27 153 35 899 

Sorted Array
1 9 20 27 35 50 98 101 153 899

#include <stdio.h>

static void radixsort(int Array[], int n);
static void countingsort(int Array[], int n, int place);
static void PrintArray(int Array[], int n);

// function for radix sort
void radixsort(int Array[], int n) {
  int max = Array[0];

  //find largest element in the Array
  for (int i=1; i<n; i++) {  
    if(max < Array[i])
      max = Array[i];
  }

  //Counting sort is performed based on place. 
  //like ones place, tens place and so on.
  for (int place = 1; max/place > 0; place *= 10) 
    countingsort(Array, n, place); 
}

static void countingsort(int Array[], int n, int place) {   
  int output[n];

  //range of the number is 0-9 for each place considered.
  int freq[10] = {0};

  //count number of occurrences in freq array
  for(int i = 0; i < n; i++)
    freq[(Array[i]/place)%10]++;

  //Change count[i] so that count[i] now contains actual 
  //position of this digit in output[] 
  for (int i = 1; i < 10; i++) 
    freq[i] += freq[i - 1];     

  //Build the output array 
  for (int i = n - 1; i >= 0; i--) { 
    output[freq[(Array[i]/place)%10] - 1] = Array[i]; 
    freq[(Array[i]/place)%10]--; 
  } 

  //Copy the output array to the input Array, Now the Array will 
  //contain sorted array based on digit at specified place
  for (int i = 0; i < n; i++) 
    Array[i] = output[i]; 
}

// function to print array
static void PrintArray(int Array[], int n) { 
  for (int i=0; i<n; i++) 
    printf("%i ",Array[i]); 
  printf("\n"); 
} 

// test the code
int main (){
  int MyArray[] = {101, 1, 20, 50, 9, 98, 27, 153, 35, 899};
  int n = sizeof(MyArray) / sizeof(MyArray[0]); 
  printf("Original Array\n");
  PrintArray(MyArray, n);


  radixsort(MyArray, n);
  printf("\nSorted Array\n");
  PrintArray(MyArray, n);
  return 0;
}

The above code will give the following output:

Original Array
101 1 20 50 9 98 27 153 35 899 

Sorted Array
1 9 20 27 35 50 98 101 153 899

using System;
   
class MyProgram {
  // function for radix sort
  static void radixsort(int[] Array) {
    int n = Array.Length;
    int max = Array[0];

    //find largest element in the Array
    for (int i=1; i<n; i++) {  
      if(max < Array[i])
        max = Array[i];
    }

    //Counting sort is performed based on place. 
    //like ones place, tens place and so on.
    for (int place = 1; max/place > 0; place *= 10) 
      countingsort(Array, place); 
  }

  static void countingsort(int[] Array, int place) {   
    int n = Array.Length;    
    int[] output = new int[n];

    //range of the number is 0-9 for each place considered.
    int[] freq = {0, 0, 0, 0, 0, 0, 0, 0, 0, 0};

    //count number of occurrences in freq array
    for(int i = 0; i < n; i++)
      freq[(Array[i]/place)%10]++;

    //Change count[i] so that count[i] now contains actual 
    //position of this digit in output[] 
    for (int i = 1; i < 10; i++) 
        freq[i] += freq[i - 1];     

    //Build the output array 
    for (int i = n - 1; i >= 0; i--) { 
      output[freq[(Array[i]/place)%10] - 1] = Array[i]; 
      freq[(Array[i]/place)%10]--; 
    } 

    //Copy the output array to the input Array, Now the Array will 
    //contain sorted array based on digit at specified place
    for (int i = 0; i < n; i++) 
      Array[i] = output[i]; 
  }

  // function to print array
  static void PrintArray(int[] Array) { 
    int n = Array.Length; 
    for (int i=0; i<n; i++) 
      Console.Write(Array[i] + " "); 
    Console.Write("\n"); 
  } 

  // test the code
  static void Main(string[] args) {
    int[] MyArray = {101, 1, 20, 50, 9, 98, 27, 153, 35, 899};
    Console.Write("Original Array\n");
    PrintArray(MyArray);

    radixsort(MyArray);
    Console.Write("\nSorted Array\n");
    PrintArray(MyArray);  
  }
}

The above code will give the following output:

Original Array
101 1 20 50 9 98 27 153 35 899 

Sorted Array
1 9 20 27 35 50 98 101 153 899

<?php
// function for radix sort
function radixsort(&$Array, $n) {
  $max = $Array[0];

  //find largest element in the Array
  for ($i=1; $i<$n; $i++) {  
    if($max < $Array[$i])
      $max = $Array[$i];
  }

  //Counting sort is performed based on place. 
  //like ones place, tens place and so on.
  for ($place = 1; $max/$place > 0; $place *= 10) 
    countingsort($Array, $n, $place); 
 }

function countingsort(&$Array, $n, $place) {   
  $output = array_fill(0,$n,0);

  //range of the number is 0-9 for each place considered.
  $freq = array_fill(0,10,0);

  //count number of occurrences in freq array
  for($i = 0; $i < $n; $i++)
    $freq[($Array[$i]/$place)%10]++;

  //Change count[i] so that count[i] now contains actual 
  //position of this digit in output[] 
  for ($i = 1; $i < 10; $i++) 
    $freq[$i] += $freq[$i - 1];    

  //Build the output array 
  for ($i = $n - 1; $i >= 0; $i--) { 
    $output[$freq[($Array[$i]/$place)%10] - 1] = $Array[$i]; 
    $freq[($Array[$i]/$place)%10]--; 
  }  
     
  //Copy the output array to the input Array, Now the Array will 
  //contain sorted array based on digit at specified place
  for ($i = 0; $i < $n; $i++) 
    $Array[$i] = $output[$i]; 
}
  
// function to print array
function PrintArray($Array, $n) { 
  for ($i = 0; $i < $n; $i++) 
    echo $Array[$i]." "; 
  echo "\n"; 
} 

// test the code
$MyArray = array(101, 1, 20, 50, 9, 98, 27, 153, 35, 899);
$n = sizeof($MyArray); 
echo "Original Array\n";
PrintArray($MyArray, $n);

radixsort($MyArray, $n);
echo "\nSorted Array\n";
PrintArray($MyArray, $n);
?>

The above code will give the following output:

Original Array
101 1 20 50 9 98 27 153 35 899 

Sorted Array
1 9 20 27 35 50 98 101 153 899

Time Complexity:

The time complexity of radix sort is Θ((N+b)*log_b(max)) in all cases, where:

N is the number of elements in unsorted array.
b is the base of input array, for example, for decimal system, b is 10.
max is the maximum element of the input array.

AlphaCodingSkills

AlphaCodingSkills Android App

AlphaCodingSkills is a online learning portal that provides tutorials on Python, Java, C++, C, C#, PHP, R, Ruby, Rust, Scala, Swift, Perl, SQL, Data Structures and Algorithms. Tutorials, examples, references and content of the website are reviewed and simplified continuously to improve comprehensibility and eliminate any possible error. We use cookies to ensure best browsing experience on our website. While using this website, you acknowledge to have read and accepted our cookie and privacy policy.