Java Program - Counting Sort

Counting sort is based on the idea that the number of occurrences of distinct elements is counted and stored in another array (say frequency array), by mapping the value of the distinct elements with index numbers of the array. The frequency array is then iterated over to use distinct elements and their occurrences and put them into the output array in a sorted way.

Example:

To understand the counting sort, lets consider an unsorted array A = [9, 1, 2, 5, 9, 9, 2, 1, 3, 3] and discuss each step taken to sort the array in ascending order.

Step 1: In this step, the largest element of the A[ ] is found out which is (9) and an another array called frequency is initiated with size [max(A[ ])+1]. Then the array A[ ] is iterated over to store the number of occurrences of each distinct element in frequency array, by mapping the distinct elements with index number of frequency array.

Step 2: In this step, the frequency array is iterated over to get the information about each distinct element and its occurrences which is further used to build the sorted array.

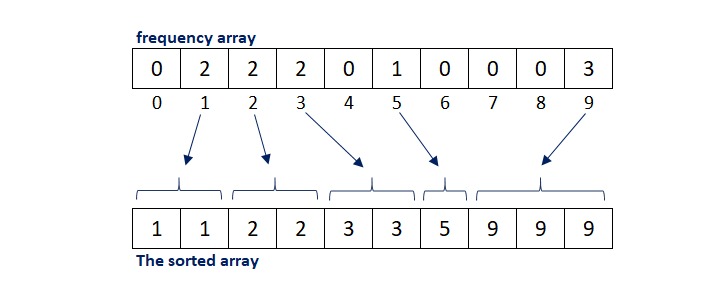
Counting sort is used most efficiently when the range of input elements is not significantly larger than the number of elements to be sorted. Along with this, the same concept can be used with negative input data as well.

Implementation of Counting Sort

public class MyClass {
  // function for counting sort
  static void countingsort(int Array[]) {
    int n = Array.length;
    int max = 0;

    //find largest element in the Array
    for (int i=0; i<n; i++) {  
      if(max < Array[i])
        max = Array[i];
    }

    //Create a freq array to store number of occurrences of 
    //each unique elements in the given array 
    int[] freq = new int[max+1];
    for (int i=0; i<max+1; i++)   
      freq[i] = 0;

    for (int i=0; i<n; i++) 
      freq[Array[i]]++;

    //sort the given array using freq array
    for (int i=0, j=0; i<=max; i++) {  
      while(freq[i]>0) { 
        Array[j] = i;
        j++;
        freq[i]--;
      }
    }
  }

  // function to print array
  static void PrintArray(int Array[])  { 
    int n = Array.length; 
    for (int i=0; i<n; i++) 
      System.out.print(Array[i] + " "); 
    System.out.println(); 
  } 

  // test the code
  public static void main(String[] args) {
    int[] MyArray =  {9, 1, 2, 5, 9, 9, 2, 1, 3, 3};
    System.out.println("Original Array");
    PrintArray(MyArray);

    countingsort(MyArray);
    System.out.println("\nSorted Array");
    PrintArray(MyArray);  
  }
}

The above code will give the following output:

Original Array
9 1 2 5 9 9 2 1 3 3 

Sorted Array
1 1 2 2 3 3 5 9 9 9 

Time Complexity:

The time complexity to iterate over the input data is Θ(N), where N is the number of elements in unsorted array and the time complexity to iterate over the frequency array is Θ(K), where K is the range of input data. The overall time complexity of counting sort is Θ(N+K) in all cases.