PHP Program - Merge Sort

Merge sort is a divide and conquer algorithm. It is based on the idea of dividing the unsorted array into several sub-array until each sub-array consists of a single element and merging those sub-array in such a way that results into a sorted array. The process step of merge sort can be summarized as follows:

• Divide: Divide the unsorted array into several sub-array until each sub-array contains only single element.
• Merge: Merge the sub-arrays in such way that results into sorted array and merge until achieves the original array.
• Merging technique: the first element of the two sub-arrays is considered and compared. For ascending order sorting, the element with smaller value is taken from the sub-array and becomes a new element of the sorted array. This process is repeated until both sub-array are emptied and the merged array becomes sorted array.

Example:

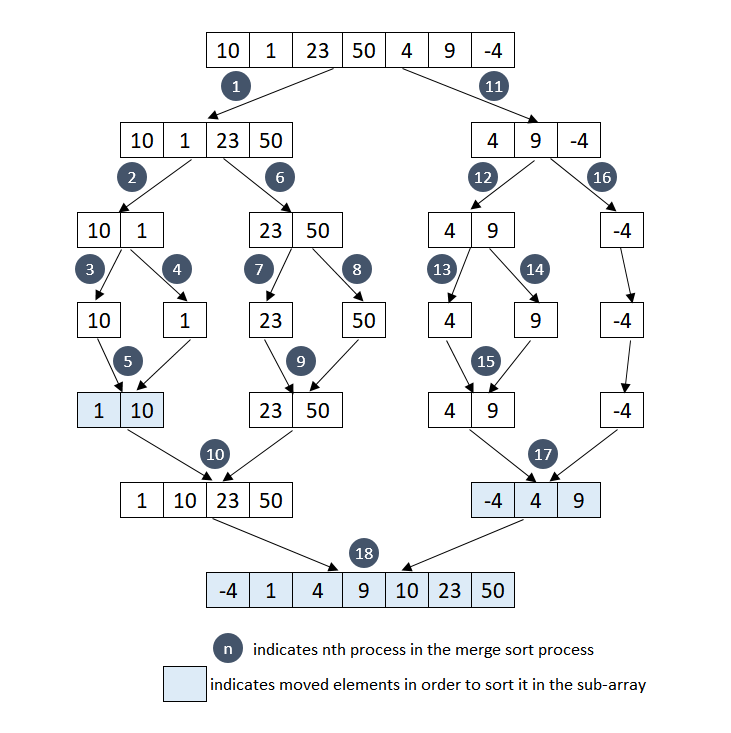
To understand the merge sort, lets consider an unsorted array [4, 9, -4] (right side array created after 11th process in the below diagram) and discuss each step taken to sort the array in ascending order.

At the first step, the array [4, 9, -4] is divided into two sub-array. The first sub-array contains [4, 9] and second sub-array contains [-4]. As the number of element in the first sub-array is greater than one, it is further divided into sub-arrays consisting of elements [4] and [9] respectively. As the number of elements in all sub-arrays is one, hence the further dividing of the array can not be done.

In the merging process, The sub-arrays formed in the last step are combined together using the process mentioned above to form a sorted array. First, [4] and [9] sub-arrays are merged together to form a sorted sub-array [4, 9]. Then [4, 9] and [-4] sub-arrays are merged together to form final sorted array [-4, 4, 9]

Implementation of Merge Sort

<?php
// function for merge sort - splits the array 
// and call merge function to sort and merge the array
// mergesort is a recursive function
function mergesort(&$Array, $left, $right) {
  if ($left < $right) { 
    $mid = $left + (int)(($right - $left)/2);
    mergesort($Array, $left, $mid);
    mergesort($Array, $mid+1, $right);
    merge($Array, $left, $mid, $right);
  }
}

// merge function performs sort and merge operations
// for mergesort function
function merge(&$Array, $left, $mid, $right) {
  // Create two temporary array to hold split 
  // elements of main array 
  $n1 = $mid - $left + 1; //no of elements in LeftArray
  $n2 = $right - $mid;     //no of elements in RightArray    
  $LeftArray = array_fill(0, $n1, 0); 
  $RightArray = array_fill(0, $n2, 0);
  for($i=0; $i < $n1; $i++) { 
    $LeftArray[$i] = $Array[$left + $i];
  }
  for($i=0; $i < $n2; $i++) { 
    $RightArray[$i] = $Array[$mid + $i + 1];
  }

  // In below section x, y and z represents index number
  // of LeftArray, RightArray and Array respectively
  $x=0; $y=0; $z=$left;
  while($x < $n1 && $y < $n2) {
    if($LeftArray[$x] < $RightArray[$y]) { 
      $Array[$z] = $LeftArray[$x]; 
      $x++; 
    }
    else { 
      $Array[$z] = $RightArray[$y];  
      $y++; 
    }
    $z++;
  }

  // Copying the remaining elements of LeftArray
  while($x < $n1) { 
     $Array[$z] = $LeftArray[$x];  
     $x++;  
     $z++;
  }

  // Copying the remaining elements of RightArray
  while($y < $n2) { 
    $Array[$z] = $RightArray[$y]; 
    $y++;  
    $z++; 
  }
}

// function to print array
function PrintArray($Array, $n) { 
  for ($i = 0; $i < $n; $i++) 
    echo $Array[$i]." "; 
  echo "\n";
} 

// test the code
$MyArray = array(10, 1, 23, 50, 4, 9, -4);
$n = sizeof($MyArray); 
echo "Original Array\n";
PrintArray($MyArray, $n);

mergesort($MyArray, 0, $n-1);
echo "\nSorted Array\n";
PrintArray($MyArray, $n);
?>

The above code will give the following output:

Original Array
10 1 23 50 4 9 -4 

Sorted Array
-4 1 4 9 10 23 50

Time Complexity:

In all cases (worst, average and best), merge sort always divides the array until all sub-arrays contains single element and takes linear time to merge those sub-arrays. Dividing process has time complexity Θ(logN) and merging process has time complexity Θ(N). Therefore, in all cases, the time complexity of merge sort is Θ(NlogN).