SciPy - Logistic Distribution

Logistic distribution is a continuous probability distribution. Its cumulative distribution function is the logistic function, which appears in logistic regression and feedforward neural networks. It resembles the logistic distribution in shape but has heavier tails.

The probability density function (pdf) of logistic distribution is defined as:

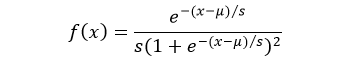
Where, μ is the mean or expectation of the distribution and s is the scale parameter of the distribution.

An exponential distribution has mean μ and variance s²𝜋²/3.

The cumulative distribution function (cdf) evaluated at x, is the probability that the random variable (X) will take a value less than or equal to x. The cdf of logistic distribution is defined as:

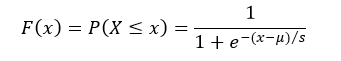
The scipy.stats.logistic contains all the methods required to generate and work with a logistic distribution. The most frequently methods are mentioned below:

Syntax

scipy.stats.logistic.pdf(x, loc=0, scale=1)
scipy.stats.logistic.cdf(x, loc=0, scale=1)
scipy.stats.logistic.ppf(q, loc=0, scale=1)
scipy.stats.logistic.rvs(loc=0, scale=1, size=1)

Parameters

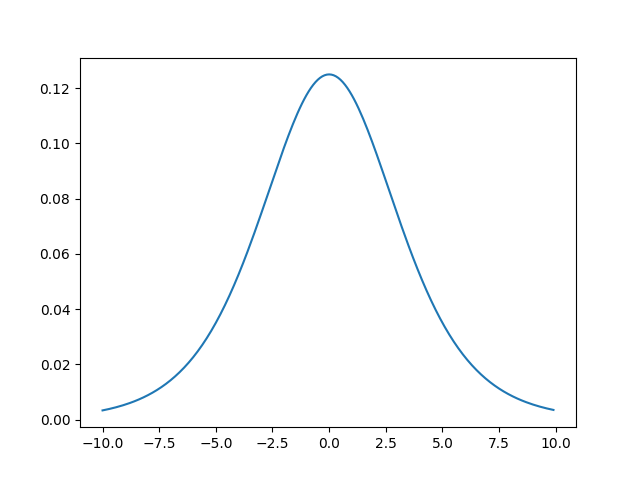
logistic.pdf()

The logistic.pdf() function measures probability density function (pdf) of the distribution.

from scipy.stats import logistic
import matplotlib.pyplot as plt
import numpy as np

#creating an array of values between
#-10 to 10 with a difference of 0.1
x = np.arange(-10, 10, 0.1)
   
y = logistic.pdf(x, 0, 2)
   
plt.plot(x, y) 
plt.show()

The output of the above code will be:

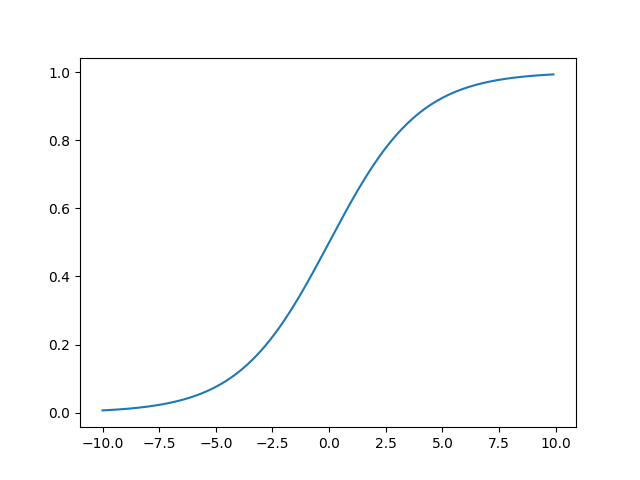
logistic.cdf()

The logistic.cdf() function returns cumulative distribution function (cdf) of the distribution.

from scipy.stats import logistic
import matplotlib.pyplot as plt
import numpy as np

#creating an array of values between
#-10 to 10 with a difference of 0.1
x = np.arange(-10, 10, 0.1)
   
y = logistic.cdf(x, 0, 2)
   
plt.plot(x, y) 
plt.show()

The output of the above code will be:

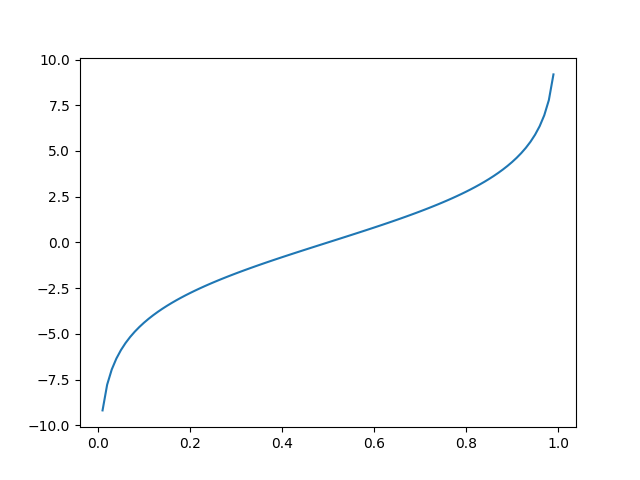
logistic.ppf()

The logistic.ppf() function takes the probability value and returns cumulative value corresponding to probability value of the distribution.

from scipy.stats import logistic
import matplotlib.pyplot as plt
import numpy as np

#creating an array of probability from
#0 to 1 with a difference of 0.01
x = np.arange(0, 1, 0.01)
   
y = logistic.ppf(x, 0, 2)
   
plt.plot(x, y) 
plt.show()

The output of the above code will be:

logistic.rvs()

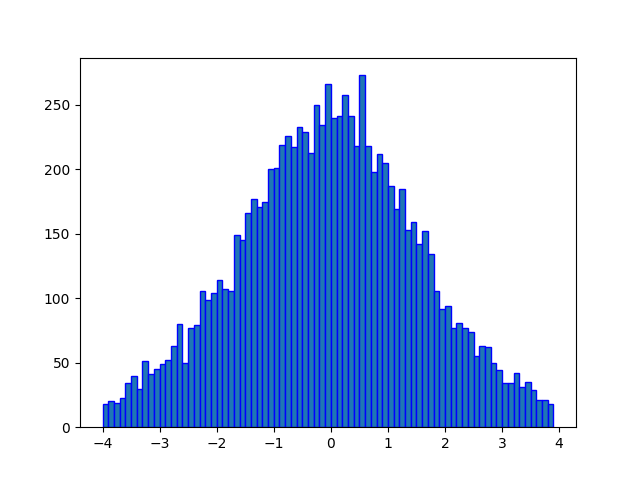
The logistic.ppf() function generates an array containing specified number of random numbers of the given logistic distribution. In the example below, a histogram is plotted to visualize the result.

from scipy.stats import logistic
import matplotlib.pyplot as plt
import numpy as np

#fixing the seed for reproducibility
#of the result
np.random.seed(10)

#creating a vector containing 10000
#logisticly distributed random numbers
y = logistic.rvs(0, 1, 10000)

#creating bin
bin = np.arange(-4,4,0.1)  

plt.hist(y, bins=bin, edgecolor='blue') 
plt.show()

The output of the above code will be: