C# Program - Quick Sort

Quick sort is a divide and conquer algorithm. It is based on the idea of choosing one element as a pivot and partitioning the array around the pivot with left side of the pivot containing all elements less than the pivot and right side of the pivot containing all elements greater than the pivot. There are many ways to choose the pivot. Few of them are mentioned below:

• First element of the array
• Last element of the array
• Random element of the array
• Median index element of the array

The quick sort has less space complexity as compared to merged sort because it do not use auxiliary array.

Example:

To understand the quick sort, lets consider an unsorted array [-4, 1, 25, 50, 8, 10, 23] and discuss each step taken to sort the array in ascending order.

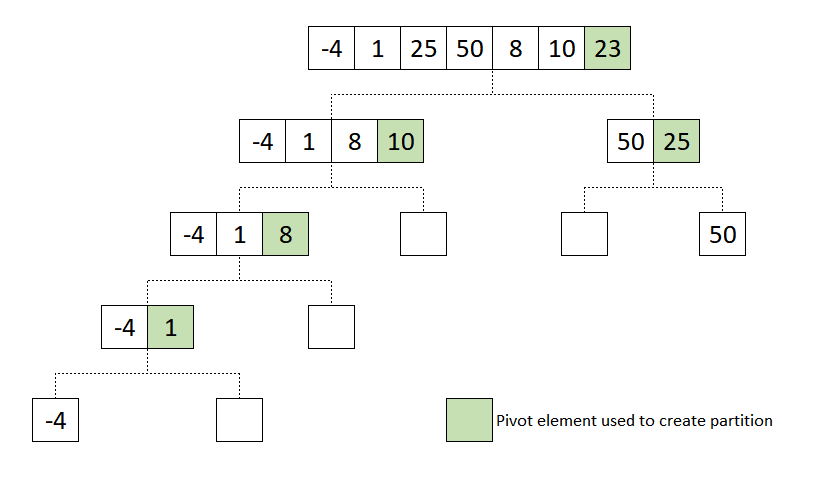
In the implementation of this example, the last element of the array is chosen as the pivot element. At the start of the partition process, variables i and j are created which are the same initially. As the partition progresses the value of i and j becomes different. i signifies the boundary between elements less than the pivot and elements greater than pivot. j signifies the boundary between elements greater than pivot and unpartitioned array.

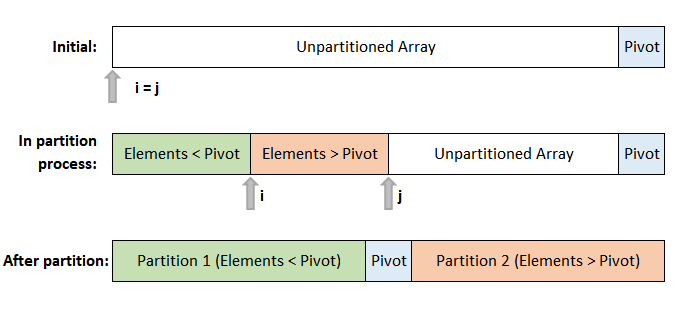
After partition, it generates two partition with left side partition contains elements less than pivot and right side partition contains elements greater than pivot. The both partition are again partitioned with the same logic and this process continues till a partition has zero or one element. The final outcome of this process will be a sorted array.

Implementation of Quick Sort

using System;

class MyProgram {
  // function for quick sort which calls partition function 
  // to arrange and split the list based on pivot element
  // quicksort is a recursive function
  static void quicksort(int[] Array, int left, int right) {
    if (left < right) { 
      int pivot = partition(Array, left, right);
      quicksort(Array, left, pivot-1);
      quicksort(Array, pivot+1, right);
    }
  }

  // partition function arrange and split the list 
  // into two list based on pivot element
  // In this example, last element of list is chosen 
  // as pivot element. one list contains all elements 
  // less than the pivot element another list contains 
  // all elements greater than the pivot element
  static int partition(int[] Array, int left, int right) {
    int i = left;
    int pivot = Array[right];
    int temp;

    for(int j = left; j <=right; j++) {
      if(Array[j] < pivot) {
        temp = Array[i];
        Array[i] = Array[j];
        Array[j] = temp;
        i++;
      }
    }

    temp = Array[right];
    Array[right] = Array[i];
    Array[i] = temp;
    return i;
  }
       
  // function to print array
  static void PrintArray(int[] Array) { 
    int n = Array.Length; 
    for (int i=0; i<n; i++)   
      Console.Write(Array[i] + " "); 
    Console.Write("\n"); 
  } 

  // test the code
  static void Main(string[] args) {
    int[] MyArray = {-4, 1, 25, 50, 8, 10, 23};
    int n = MyArray.Length;
    Console.Write("Original Array\n");
    PrintArray(MyArray);

    quicksort(MyArray, 0, n-1);
    Console.Write("\nSorted Array\n");
    PrintArray(MyArray);  
  }
}

The above code will give the following output:

Original Array
-4 1 25 50 8 10 23 

Sorted Array
-4 1 8 10 23 25 50 

Time Complexity:

The time complexity of quick sort is Θ(N²) in worst case and the time complexity in best and average cases are Θ(NlogN).