C# Program - Shell Sort

The Shell sort is based on the idea that farther elements are sorted first and successively decrease the interval between the elements to be sorted. It is a generalized version of insertion sort. In shell sort, elements at specific interval are sorted first and the interval is gradually decreased until it becomes one. There are many ways to choose interval for shell sort and few of them are listed below. Please note that the performance of shell sort depends upon type of sequence chosen.

• Shell’s original sequence: N/2, N/4, …, 1
• Knuth’s sequence: 1, 4, 13, …, (3n – 1) / 2
• Sedgewick’s sequence: 1, 8, 23, 77, 281...
• Hibbard’s sequence: 1, 3, 7, 15, 31, 63…

Example:

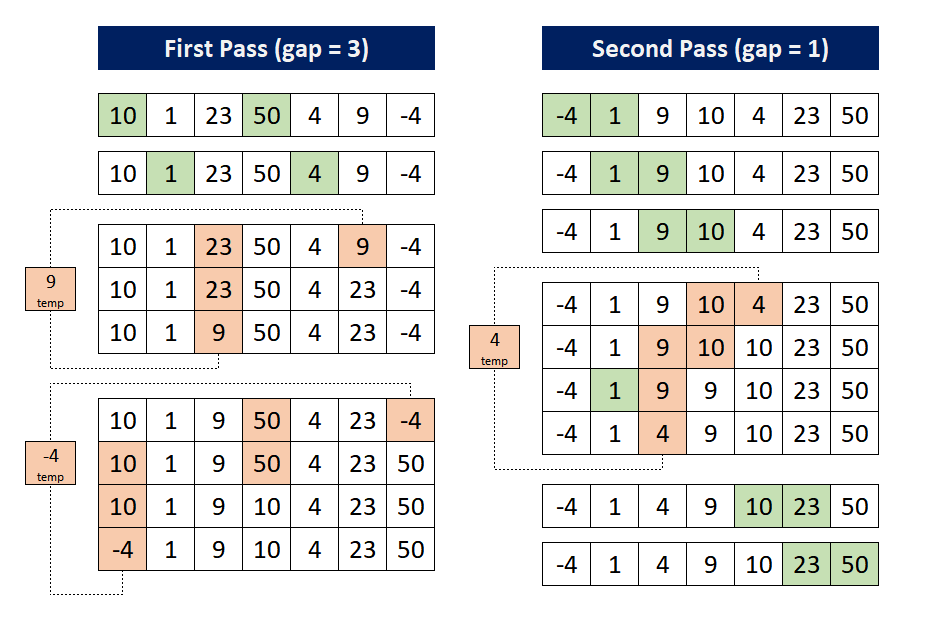
To understand the Shell sort, lets consider an unsorted array [10, 1, 23, 50, 4, 9, -4] and discuss each step taken to sort the array in ascending order. In this example, Shell's original sequence is considered hence the intervals (gaps) will be three and one (N=7).

First Pass: For this pass, the gap size is three. Hence, the first element (10) is compared with fourth element (50) and found in the correct order. Then the second element (1) is compared with fifth element (4) which are also in the correct order. Then, the third element (23) is compared with the sixth element (9), since (23 > 9), the sixth element is replaced by (23) and (9) is stored in a temp variable. As, third - gap = 0. Hence there is no element which can be compared with temp, therefore, the third term will be replaced by temp.

After that, the fourth element (50) is compared with the seventh element (-4), since (50 > -4), the seventh element is replaced by (50) and (-4) is stored in a temp variable. As, fourth - gap = 1, hence, the temp is again compared with first element (10). since (10 > -4), the fourth element is replaced by (10) and first element is replaced by temp (there is no element which can be compared with temp).

Second Pass: For this pass gap size is one. First four elements are already sorted. After that, the fourth element (10) is compared with the fifth element (4), since (10 > 4), the fifth element is replaced by (10) and (4) is stored in a temp variable. Now, the temp is compared with third element (9) which is greater than temp, hence fourth element is replaced by (9). Then, the temp is compared with second element (1) which is less than temp, hence third element is replaced by temp. After that, sixth and seventh elements are also considered for comparison which are already sorted.

Implementation of Shell Sort

using System;

class MyProgram {
  // function for shell sort
  static void shellsort(int[] Array) {
    int n = Array.Length;
    int gap = n/2;
    int temp, i, j;
    while(gap > 0) {
      for(i = gap; i < n; i++) {
        temp = Array[i];
        j = i;
        while(j >= gap && Array[j-gap] > temp) {
          Array[j] = Array[j-gap];
          j = j - gap;  
        }
        Array[j] = temp;
      }
      gap = gap / 2;
    }
  }

  // function to print array
  static void PrintArray(int[] Array) { 
    int n = Array.Length; 
    for (int i=0; i<n; i++)   
      Console.Write(Array[i] + " "); 
    Console.Write("\n"); 
  } 

  // test the code
  static void Main(string[] args) {
    int[] MyArray = {10, 1, 23, 50, 4, 9, -4};
    Console.Write("Original Array\n");
    PrintArray(MyArray);

    shellsort(MyArray);
    Console.Write("\nSorted Array\n");
    PrintArray(MyArray);  
  }
}

The above code will give the following output:

Original Array
10 1 23 50 4 9 -4 

Sorted Array
-4 1 4 9 10 23 50

Time Complexity:

In above implementation, the time complexity of shell sort in worst case scenario is Θ(N²) and the time complexity in best and average case scenarios are Θ(NlogN). There are various methods to consider gap which lead to better time complexity.