Python Program - Heap Sort

Heap sort uses property of heap to sort the array. It involves building a max heap for increasing order sorting which contains largest element of the heap at the root. For decreasing order sorting min heap is used which contains smallest element of the heap at the root. The process step of for increasing order sorting of heap sort is summarized below:

• Step 1: Build a max heap which contains largest element of the heap at the root
• Step 2: Swap the last element of heap with root element and remove the last element from the heap. With the remaining elements repeat the step 1.

Example:

To understand the heap sort, lets consider an unsorted array [10, 1, 23, 50, 7, -4] and discuss each step taken to sort the array in ascending order.

In the below figure, the heap structure of input array and max heap is shown. The index number of the root element of the heap is 0. In max heap, the largest element of the heap always resides at the root.

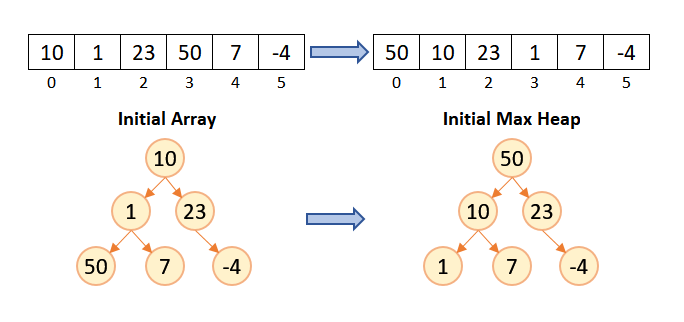
After building the initial max heap, the last element of heap is swapped with the root element and the last element which contains the largest number of the array is removed from the heap. After that, the heapify function is used on the remaining elements of the heap to make it as a max heap and the number of elements will reduce by one. This process is continued until the number of elements in the heap is one. At this point, the array will be sorted.

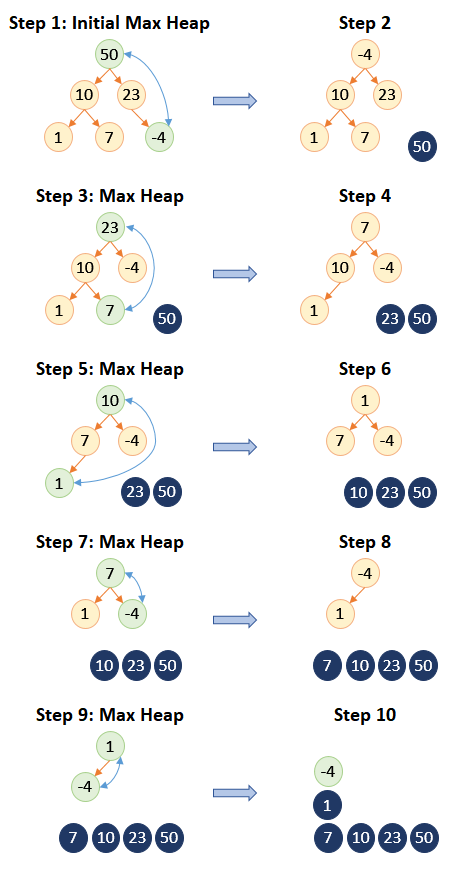
The above figure describes elimination of largest element from the heap and formation of the max heap from the remaining elements of the heap. The final outcome of the process is an increasing order sorted array.

Implementation of Heap Sort

# function for heap sort which calls heapify function 
# to build the max heap and then swap last element of 
# the max-heap with the first element
# exclude the last element from the heap and rebuild the heap
def heapsort(MyList):
  n = len(MyList)
  for i in range(n//2, -1, -1):
    heapify(MyList, n-1, i)

  for i in range(n-1, -1, -1):
    # swap last element of the max-heap with the first element
    MyList[i], MyList[0] = MyList[0], MyList[i]
    
    # exclude the last element from the heap and rebuild the heap 
    heapify(MyList, i-1, 0)

# heapify function is used to build the max heap
# max heap has maximum element at the root which means
# first element of the array will be maximum in max heap
def heapify(MyList, n, i):
  max, left, right = i, 2*i + 1, 2*i + 2
  # if the left element is greater than root
  if left <= n and MyList[left] > MyList[max]:
    max = left

  # if the right element is greater than root
  if right <= n and MyList[right] > MyList[max]:
    max = right

  # if the max is not i
  if max != i:
    MyList[i], MyList[max] = MyList[max], MyList[i]
    # Recursively heapify the affected sub-tree
    heapify(MyList, n, max) 

# function to print list
def PrintList(MyList):
  for i in MyList:
    print(i, end=" ")
  print("\n")
  
# test the code                 
MyList = [10, 1, 23, 50, 7, -4]
n = len(MyList)
print("Original List")
PrintList(MyList)

heapsort(MyList)
print("Sorted List")
PrintList(MyList)

The above code will give the following output:

Original List
10 1 23 50 7 -4 

Sorted List
-4 1 7 10 23 50

Time Complexity:

The time complexity of creating a heap is Θ(N) and time complexity of creating a max heap is Θ(logN) and overall time complexity of heap sort is Θ(NlogN).