Python Program - Radix Sort

Radix sort is based on the idea that the sorting of the input data is done digit by digit from least significant digit to most significant digit and it uses counting sort as a subroutine to perform sorting. Counting sort is a linear sorting algorithm with overall time complexity Θ(N+K) in all cases, where N is the number of elements in the unsorted array and K is the range of input data. The idea of radix sort is to extend the counting sort algorithm to get a better time complexity when K goes up.

Example:

To understand the radix sort, lets consider an unsorted array A = [101, 1, 20, 50, 9, 98, 27, 153, 35, 899] and discuss each step taken to sort the array in ascending order.

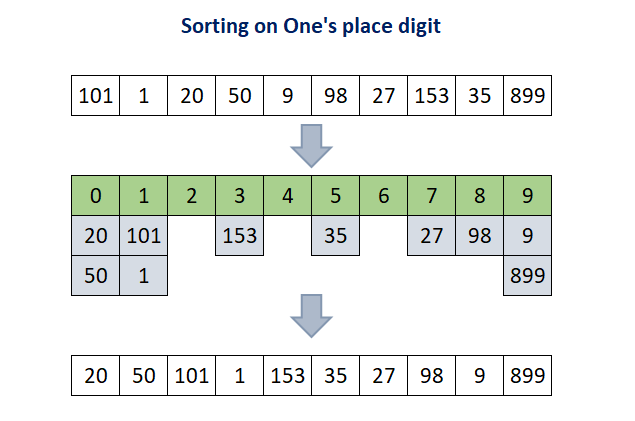
Step 1: According to the algorithms, the input data is first sorted based on least significant digit. Therefore, array A[ ] is sorted based on one's digit. After sorting it on one's digit it will become [20, 50, 101, 1, 153, 35, 27, 98, 9, 899].

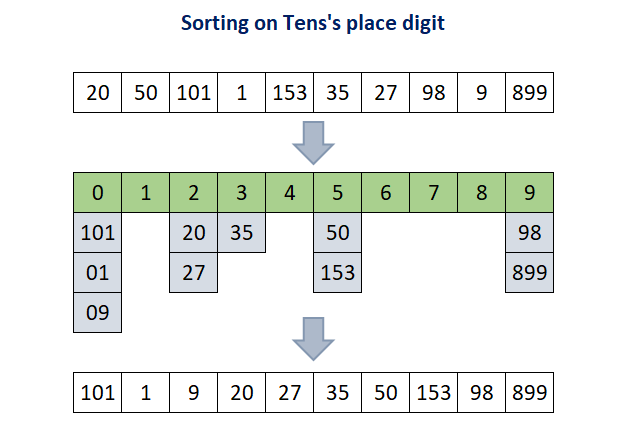
Step 2: In this step, the array A[ ] array is sorted based on ten's digit and after this step it will become [101, 1, 9, 20, 27, 35, 50, 153, 98, 899].

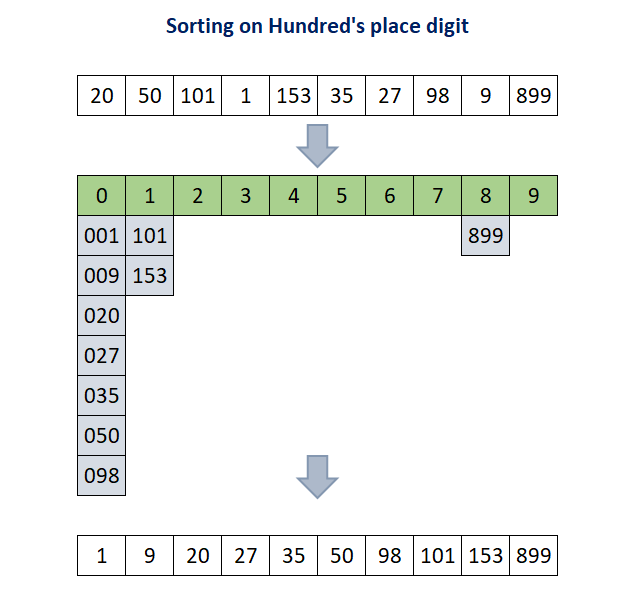
Step 3: Finally, the array A[ ] is sorted based on hundred's digit (most significant digit) and the array will be sorted after this step and the final array will be [1, 9, 20, 27, 35, 50, 98, 101, 153, 899].

Implementation of Radix Sort

# function for radix sort
def radixsort(MyList):
  n = len(MyList)
  max = MyList[0]
  
  #find largest element in the Array
  for i in MyList:
    if max < i:
      max = i
  
  #Counting sort is performed based on place. 
  #like ones place, tens place and so on.
  place = 1
  while max/place > 0:
    countingsort(MyList, place)
    place *= 10  

def countingsort(MyList, place):
  n = len(MyList)
  output = [0 for i in range(0,n)]
  
  #range of the number is 0-9 for each place considered.
  freq = [0 for i in range(0,10)]
  
  #count number of occurrences in freq array
  for i in range(0,n):
    freq[(MyList[i]//place)%10] += 1
  
  #Change count[i] so that count[i] now contains actual 
  #position of this digit in output[] 
  for i in range(1,10):
    freq[i] += freq[i - 1]      
  
  #Build the output array 
  for i in range(n-1,-1,-1):
    output[freq[(MyList[i]//place)%10] - 1] = MyList[i] 
    freq[(MyList[i]//place)%10] -= 1
  
  #Copy the output array to the input Array, Now the Array will 
  #contain sorted array based on digit at specified place
  for i in range(0,n): 
    MyList[i] = output[i]   

#print a list
def PrintList(MyList):
  for i in MyList:
    print(i, end=" ")
  print("\n") 
  
# test the code                 
MyList = [101, 1, 20, 50, 9, 98, 27, 153, 35, 899]
print("Original List")
PrintList(MyList)

radixsort(MyList)
print("Sorted List")
PrintList(MyList)

The above code will give the following output:

Original List
101 1 20 50 9 98 27 153 35 899 

Sorted List
1 9 20 27 35 50 98 101 153 899 

Time Complexity:

The time complexity of radix sort is Θ((N+b)*log_b(max)) in all cases, where:

• N is the number of elements in unsorted array.
• b is the base of input array, for example, for decimal system, b is 10.
• max is the maximum element of the input array.