NumPy - Normal Distribution

Normal (Gaussian) Distribution is a probability function that describes how the values of a variable are distributed. It is a symmetric distribution about its mean where most of the observations cluster around the mean and the probabilities for values further away from the mean taper off equally in both directions. It is the most important probability distribution function used in statistics because of its advantages in real case scenarios. For example, the height of the population, measurement errors etc.

The probability density function (pdf) of normal distribution is defined as:

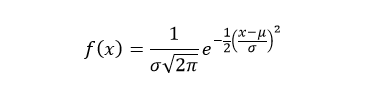
Where, μ is the mean or expectation of the distribution and σ is the standard deviation of the distribution.

An normal distribution has mean μ and variance σ². A normal distribution with μ=0 and σ=1 is called standard normal distribution.

The cumulative distribution function (cdf) evaluated at x, is the probability that the random variable (X) will take a value less than or equal to x. The cdf of normal distribution is defined as:

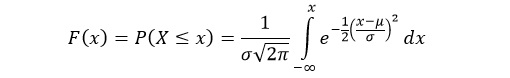
The NumPy random.normal() function returns random samples from a normal (Gaussian) distribution.

Syntax

numpy.random.normal(loc=0.0, scale=1.0, size=None)

Parameters

Return Value

Returns samples from the parameterized normal distribution. ndarray or scalar.

Example: Values from standard normal distribution

In the example below, random.normal() function is used to create a matrix of given shape containing random values drawn from standard normal distribution, N(0, 1).

import numpy as np

size = (5,3)

sample = np.random.normal(0, 1, size)
print(sample)

The possible output of the above code could be:

[[-1.50667135 -2.71170091 -0.30597761]
 [ 0.21858771 -0.67194669  0.29402538]
 [ 0.12713626 -1.78105631 -0.81233742]
 [ 1.18490393  1.29206451  1.1685965 ]
 [ 0.08644936 -1.54759699 -0.44458985]]

Plotting normal distribution

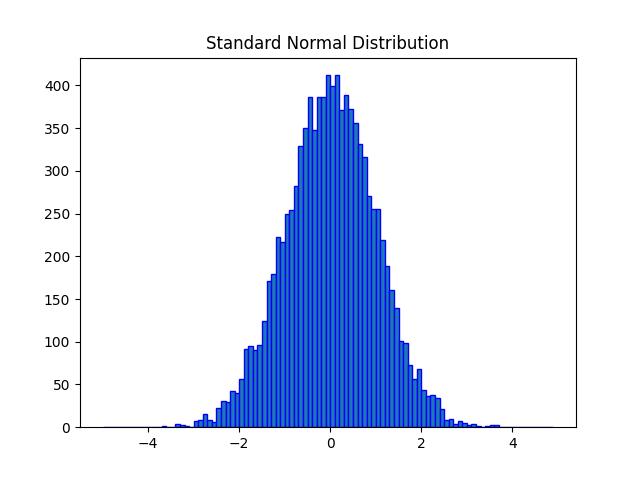
Example: Density plot

Matplotlib is a plotting library for the Python which can be used to plot the probability density function (pdf) of normal distribution using hist() function.

import matplotlib.pyplot as plt
import numpy as np

#fixing the seed for reproducibility
#of the result
np.random.seed(10)

size = 10000
#drawing 10000 sample from 
#standard normal distribution
sample = np.random.normal(0, 1, size)
bin = np.arange(-5,5,0.1)

plt.hist(sample, bins=bin, edgecolor='blue') 
plt.title("Standard Normal Distribution") 
plt.show()

The output of the above code will be:

Example: Comparing pdfs

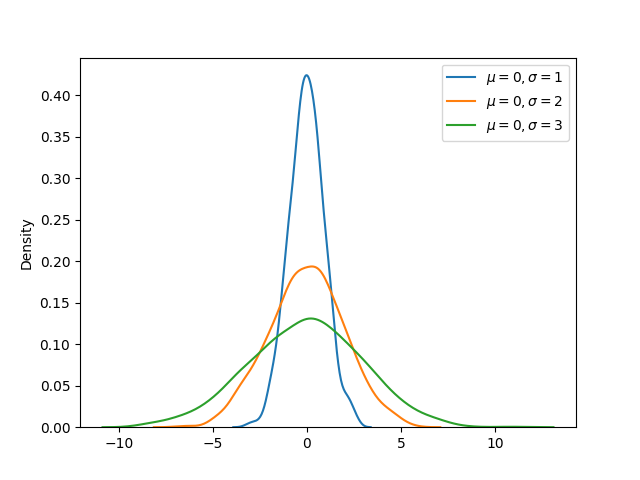
Multiple probability density functions can be compared graphically using Seaborn kdeplot() function. In the example below, pdf of three normal distributions (each with mean 0 and standard deviation 1, 2 and 3 respectively) are compared.

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

#fixing the seed for reproducibility
#of the result
np.random.seed(10)

size = 1000
#plotting 1000 sample from 
#different normal distribution
sns.kdeplot(np.random.normal(0, 1, size))
sns.kdeplot(np.random.normal(0, 2, size))
sns.kdeplot(np.random.normal(0, 3, size))

plt.legend([r"$\mu = 0, \sigma = 1$", 
            r"$\mu = 0, \sigma = 2$", 
            r"$\mu = 0, \sigma = 3$"])
plt.show()

The output of the above code will be:

Example: Comparing cdfs

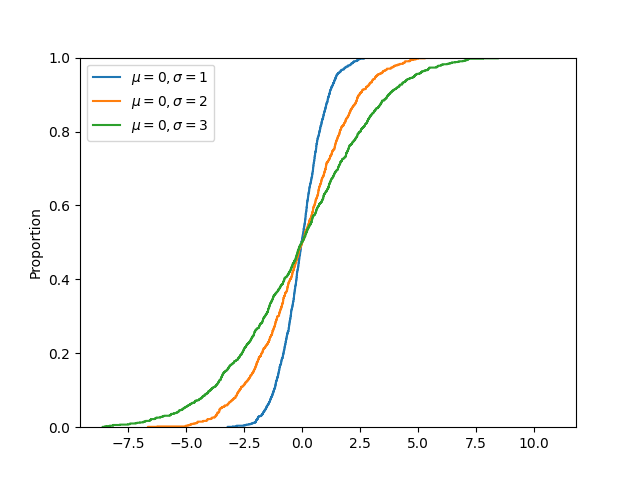
Multiple cumulative distribution functions can be compared graphically using Seaborn ecdfplot() function. In the example below, cdf of three normal distributions (each with mean 0 and standard deviation 1, 2 and 3 respectively) are compared.

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

#fixing the seed for reproducibility
#of the result
np.random.seed(10)

size = 1000
#plotting 1000 sample from 
#different normal distribution
sns.ecdfplot(np.random.normal(0, 1, size))
sns.ecdfplot(np.random.normal(0, 2, size))
sns.ecdfplot(np.random.normal(0, 3, size))

plt.legend([r"$\mu = 0, \sigma = 1$", 
            r"$\mu = 0, \sigma = 2$", 
            r"$\mu = 0, \sigma = 3$"])
plt.show()

The output of the above code will be:

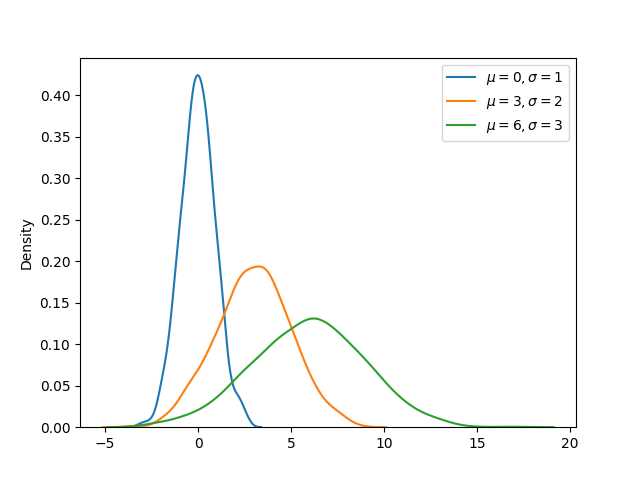
Example: comparing pdfs (different mean and std)

In the example below, three normal distributions each with different mean and standard deviations are graphically compared.

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

#fixing the seed for reproducibility
#of the result
np.random.seed(10)

size = 1000
#plotting 1000 sample from 
#different normal distribution
sns.kdeplot(np.random.normal(0, 1, size))
sns.kdeplot(np.random.normal(3, 2, size))
sns.kdeplot(np.random.normal(6, 3, size))

plt.legend([r"$\mu = 0, \sigma = 1$", 
            r"$\mu = 3, \sigma = 2$", 
            r"$\mu = 6, \sigma = 3$"])
plt.show()

The output of the above code will be: